This theme focusses on how modelling can inform the elimination and eradication of infectious diseases. There are several members of this theme, detailed in the "People" section, which have considerable experience in this area. The aim of this research theme is to:

• Share knowledge and experiences in developing mathematical models for the purpose of informing elimination and eradication
• Develop and refine methodological approaches specific to elimination and eradication.
• Develop best practice in how modelling can be used by stakeholders and policy makers working in elimination and eradication
• Improve how diagnostic tools and surveillance affects inference on elimination

Introduction

In 1997 a workshop on the Eradication of Infectious Diseases was held to discuss and define the terms elimination and eradication, identify lessons that can be learned from previous and current programs and develop the science of eradication. Mathematical models were discussed at this meeting, and their inference has been informative from the beginning. At that time, only smallpox had been eradicated after decades of intensive control efforts through use of vaccination and surveillance for outbreaks of this deadly disease. Other eradication programmes have since failed; yellow fever, malaria, and yaws.  

Since this time world has changed; there is new enthusiasm for eradication. In the 1980s polio was successfully eliminated from the Americas and enormous efforts have been undertaken to eradicate. In veterinary medicine rinderpest has not been reported in animals since 2006 and an intense serological surveillance program has confirmed eradication. Guinea-worm disease is restricted only to 4 countries in sub-Saharan Africa. For some vector-borne diseases new control tools are becoming available and eradication is once again being discussed.

These exciting public health developments require an informed analysis to help support development of feasible elimination and eradication plans. Central to this is an understanding of the feasibility of eradication and mathematical modelling can have a role. Mathematical and statistical models can be used to inform:

• The feasibility of moving from control to elimination
• Whether an epidemic will die out within a period of time
• The probability that transmission has been eliminated

Especially when there are multiple options for an intervention, it is possible to compare the interventions by estimating the probability of each preferred outcome. Common to many of these themes is the use of data from outbreaks of infectious diseases to understand disease dynamics, and how they can be altered through control activities.

Crossness Sewage Treatment trip

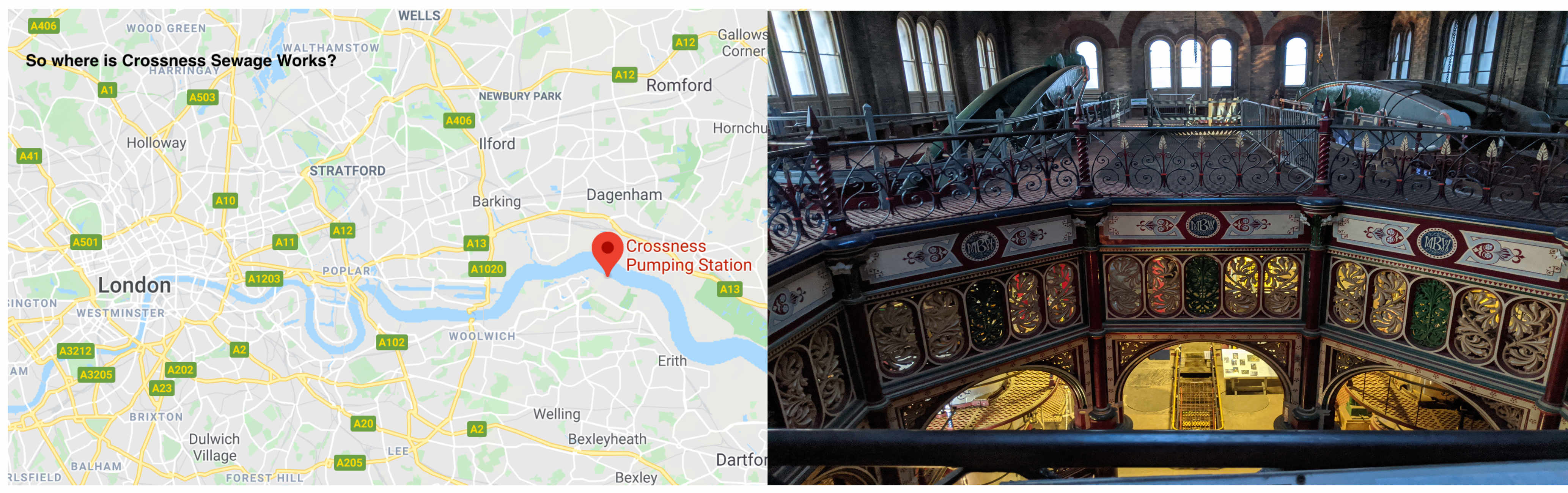
On what was possibly the coldest day in 2019 we made a trip to Crossness Sewage Treatment works to see how the Victorians dealt with London’s sewage. This is related to elimination and eradication because cholera was a huge public health problem in London before the development of considerable engineering infrastructure to remove waste from contaminating the water supply in London, and sewage sampling is a critical form of surveillance for poliovirus and other pathogens. We were shown round the old treatment works at Crossness sewage by Petra Cox (Outreach Officer). Fascinating insights included the speed at which the project was planned and implemented by Joseph Bazalgette, and the beautiful details of the inside of the pumping station.

Elimination and Eradication CMMID seminar

In July 2019, we had a very interesting set of ‘turbo talks’ by researchers within LSHTM who are working on areas linked to elimination and eradication;

The meeting allowed us to ruminate over the common threads across these diseases. It was apparent that targets, even if they will not feasibly be met are useful to catalyse progress, but we wondered if this approach will erode with time (“crying wolf” with each new target). Across many diseases it was apparent that surveillance becomes critical as the disease reduces in incidence, and it is often at this time that stakeholders and funders of surveillance may lose interest. A few examples of the ‘freedom from infection’ framework were given, which provide a useful framework to understand the importance of surveillance in near-elimination settings.

• Kath O'Reilly - Polio
• Amy Pinsent – Trachoma
• Lindsay Wu – Malaria
• Lloyd Chapman – Leishmaniasis
• Tom Sumner – Tuberculosis

Research highlights

Polio Eradication: A public health catch-22

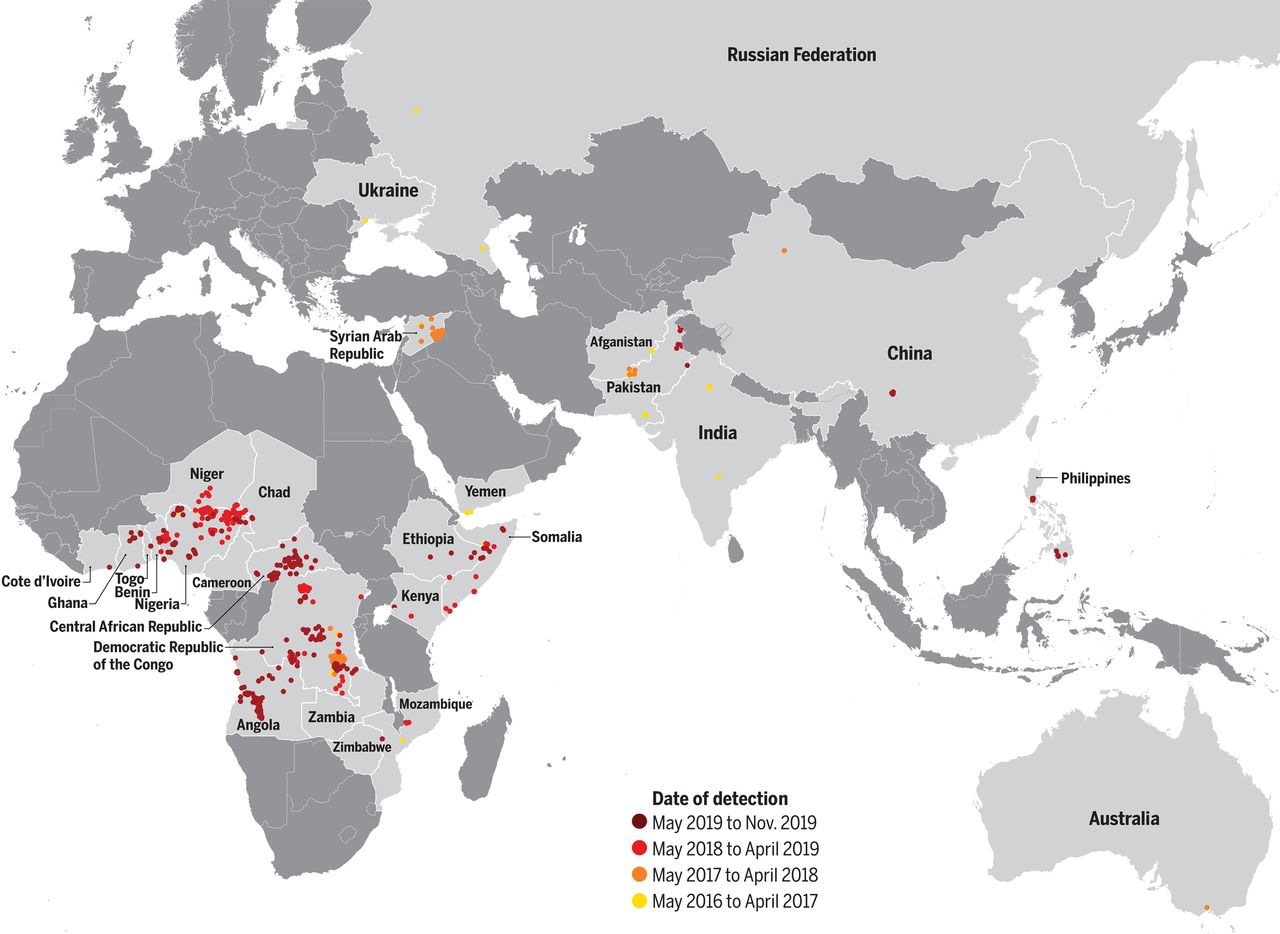
In March 2020, several researchers within the Elimination and Eradication theme published a paper in Science, describing the epidemiology and challenges of eradicating poliomyelitis. In 2016, the serotype 2 component of the oral poliovirus vaccine given to children was withdrawn. This measure was taken to prevent vaccine-associated disease outbreaks caused by mutation in the live attenuated vaccine. At the time, children around the world had lowered immunity to serotype 2 poliovirus because the inactivated vaccine is far less effective and a new oral vaccine was not yet ready. Using a statistical model, Macklin et al. discovered that most outbreaks of polio across Asia and sub-Saharan Africa are likely associated with the serotype 2 vaccine strain. To block transmission when poliovirus outbreaks occur requires deployment of the only tool in the box: the existing live attenuated serotype 2 oral vaccine, which increases the risk of vaccine-derived disease.

In late 2020 the new oral vaccine, the nOPV2, received emergency use licensure and the first use of nOPV2 in field conditions is expected to be completed in early 2021. The nOPV2 has been shown in Phase I and II trials to be considerably more genetically stable, and has the potential to be an important tool in preventing further cases of vaccine-derived disease. Research is continuing within the theme to support polio eradication through epidemiological analysis and modelling, such as that reported in a follow on paper in Vaccine and discussed in this expert opinion piece.  

Measles elimination in Europe

In a recent commentary in the Lancet, several members of CMMID suggest that measles elimination in Europe is in crisis . In 2018 within the 53 countries of the EURO region more than 80,000 confirmed cases were reported. Measles is well understood to be an acute and highly transmissible infectious disease, but also an infection with a highly immunogenic vaccine that is available through routine immunisation. There are many challenges of measles elimination, including vaccine hesitancy and issues with access to vaccines, especially in vulnerable and highly mobile populations.

In a recent analysis of data from France, Alexis Robert has illustrated that vaccine coverage is highly protective against imported cases and localised outbreaks, and regions reporting recent incidence had a lower risk of local transmission, a finding consistent with acquisition of local immunity. Importantly, the WHO criteria for measles elimination (ie. low recent incidence) was associated with a higher probably of observing cases, presumably due to a build up of susceptibility. This finding has implications for elimination assessments for measles as the criteria are inconsistent with the epidemiology of measles, and should consider important factors such as local vaccination coverage.